分布式/并行SMT求解器

可满足性模理论（SMT）在形式化方法和自动推理领域中有着广泛应用，主要研究特定理论下（如等式理论、位向量、线性与非线性算术）的一阶逻辑公式的可满足性判定。

目前，大多数研究工作聚焦于如何改进串行SMT求解器中的技术与启发式方法。然而，随着工业应用中问题的规模和复杂性不断增加，串行SMT求解器的性能已难以满足需求。而现有的SMT划分策略主要基于布尔级划分，无法充分处理具有复杂逻辑结构的公式，导致分布式SMT求解器的性能受到限制。

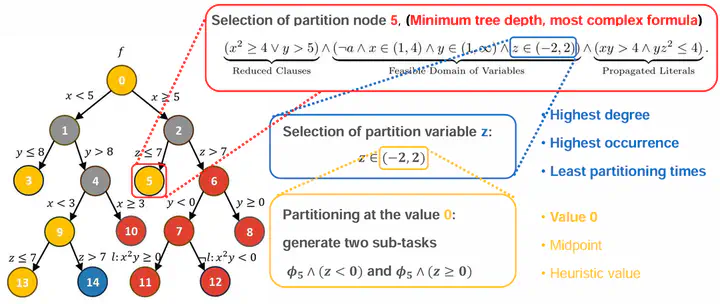
我们首次提出了一种基于变量级划分的动态分布式框架，能够有效地对任意逻辑结构的公式进行划分。针对算术理论，本文通过增强约束传播算法，并将其与布尔传播相协调，集成到变量级划分策略中，显著提升了公式简化和解空间削减的能力，从而提高了求解效率。我们将该方法应用于三个国际领先的求解器CVC5、OpenSMT2和Z3，实验结果表明，相较于基准串行求解器，应用我们的分布式技术后，平均成功求解的实例数量增加了3495个（在52471个算术理论相关测试实例中），求解速度提升了约30%。此外，在传统串行求解器无法解决的6247个实例中，我们的方法成功求解了1211个。尤其在非线性理论上，我们的方法表现出显著的优势，超越了CVC5和OpenSMT2团队开发的分布式求解技术。

该研究不仅为分而治之的并行与分布式划分方法提供了新的方向，也为其他SMT理论的变量级划分方法开辟了探索空间。并在国际权威竞赛 SMT-COMP 2024 的云赛道中获得多项冠军与“最大领先奖”、“最大贡献奖”。同时，首次提出的“基于变量级划分的动态分布式框架”也获得国际顶级形式化验证会议CAV 2024的“杰出论文奖”。